Hello, Let mathcal(S) the surface of equation z = ln(x^2y^2) it's the graph of your function f Remark that mathcal(S) is a revolution surface, because f(x,y) = g(r) where r = sqrt(x^2y^2) is the polar radius Actually, g(r) = ln(r^2) = 2 ln(r) So, graph the curve of equation z = 2ln(x) in the xOz plane
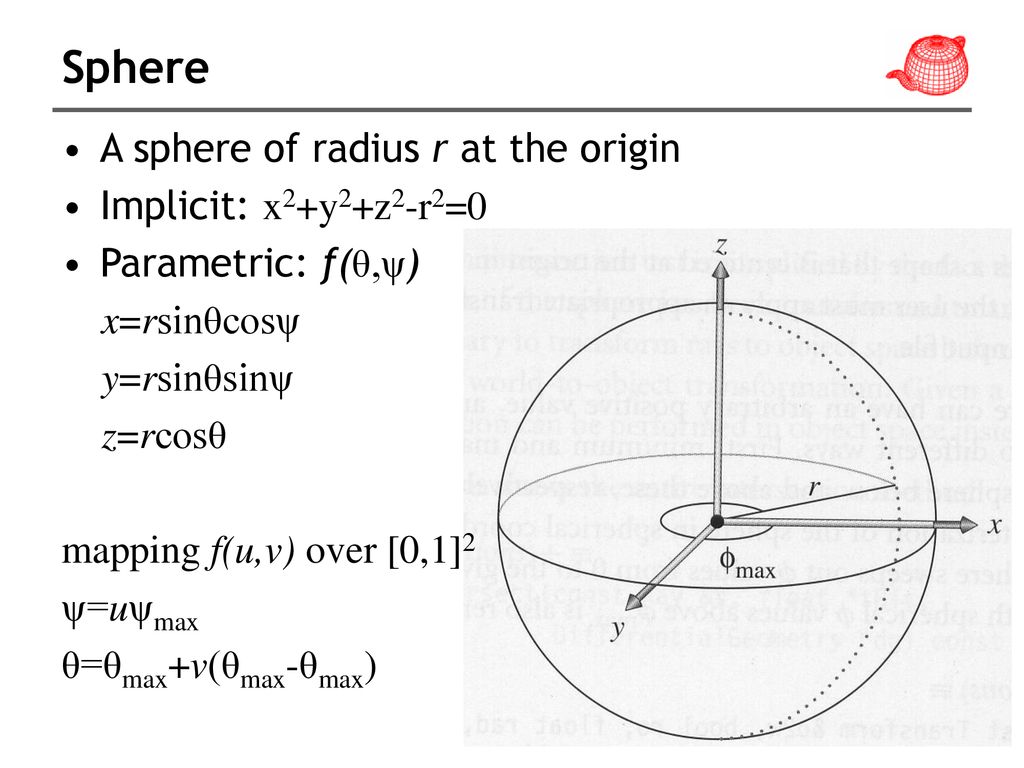
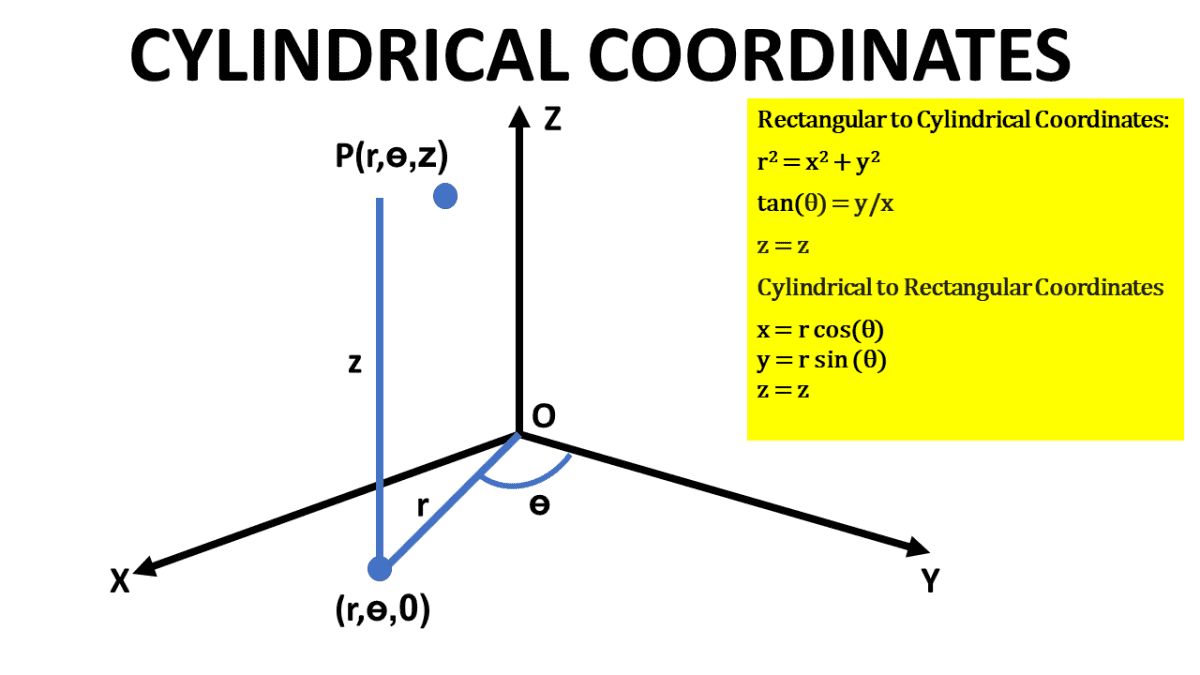
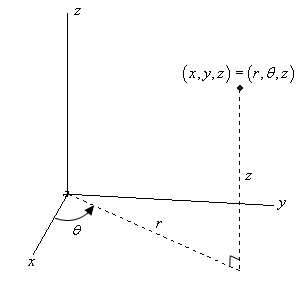
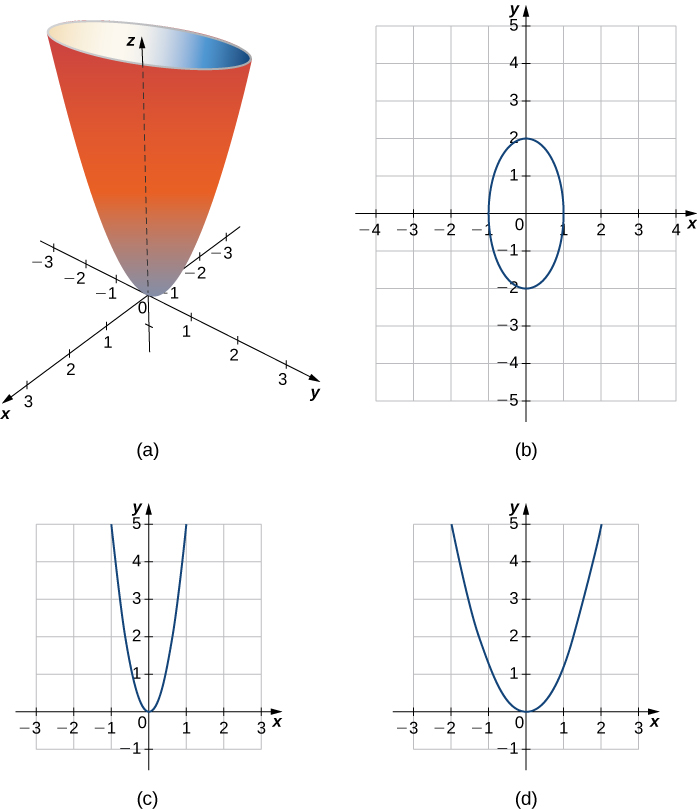
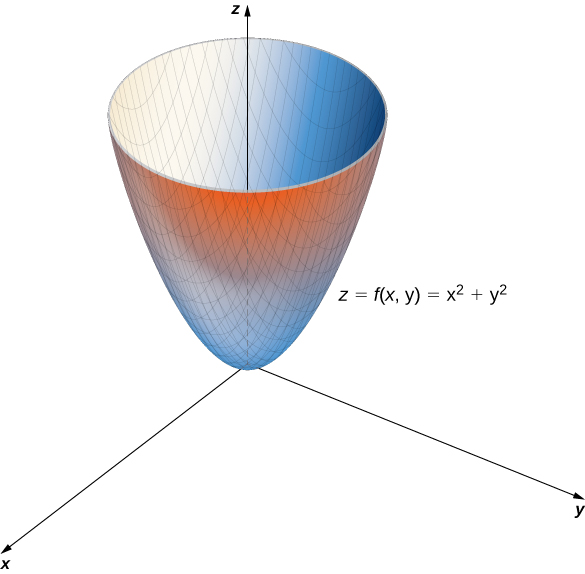
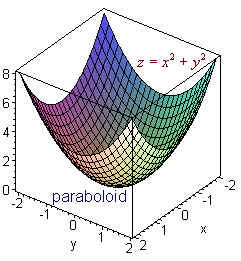
X^2+y^2+z^2=r^2 graph-Figure 2 The right triangle lies in the xyplaneThe length of the hypotenuse is r r and θ θ is the measure of the angle formed by the positive xaxis and the hypotenuseThe zcoordinate describes the location of the point above or below the xyplaneAnswer to Solved Sketch the graph of z = x^2 y^2 in R^3 Name the Transcribed image text Sketch the graph of z = x^2 y^2 in R^3 Name the surface (a) Paraboloid (b) Ellipsoid (c) Circle (d) Hyperboloid Find the domain of the function f(x, y) = ln(x y^2)
X^2+y^2+z^2=r^2 graphのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 | ||
 |  | |
「X^2+y^2+z^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「X^2+y^2+z^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「X^2+y^2+z^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「X^2+y^2+z^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「X^2+y^2+z^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「X^2+y^2+z^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「X^2+y^2+z^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「X^2+y^2+z^2=r^2 graph」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
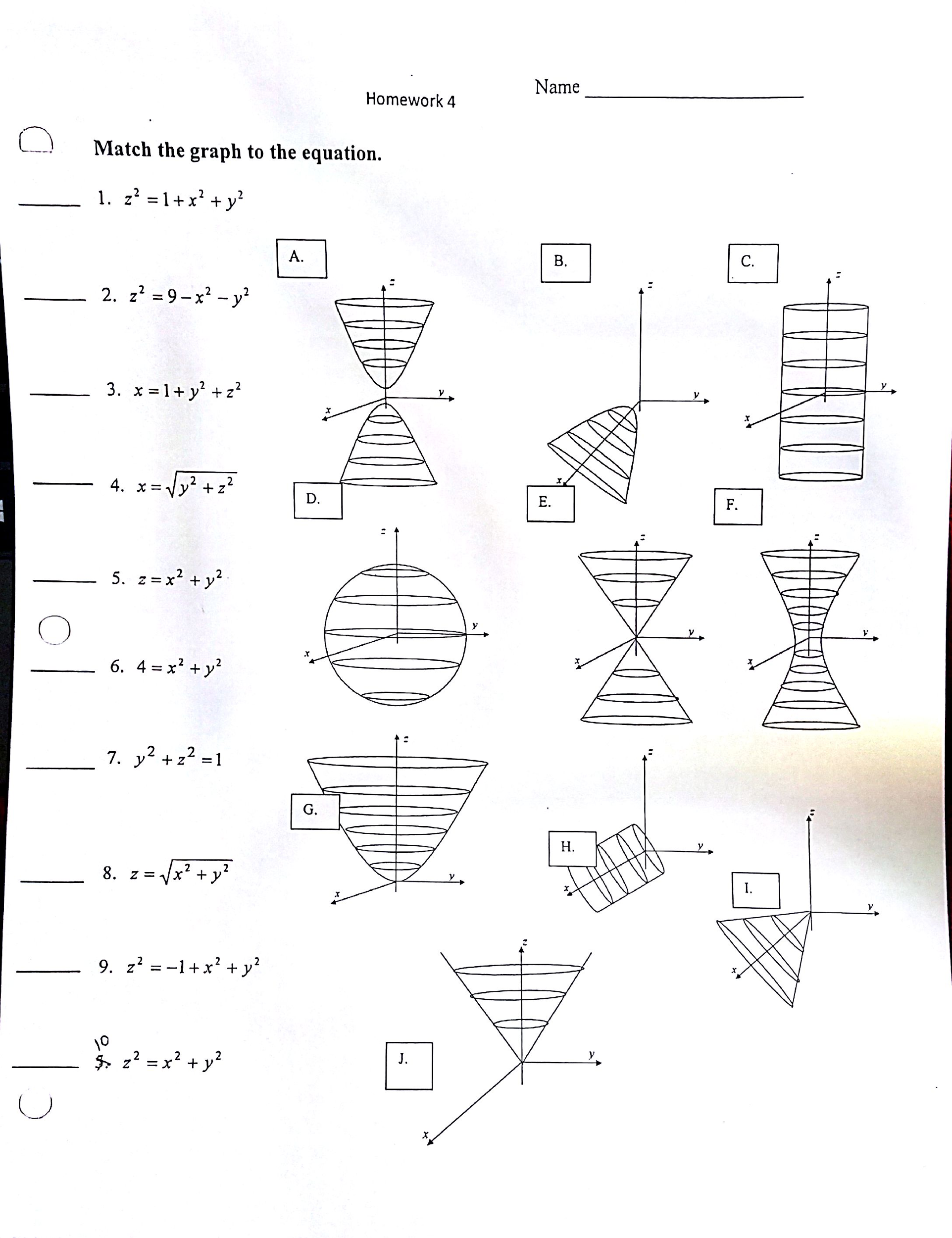
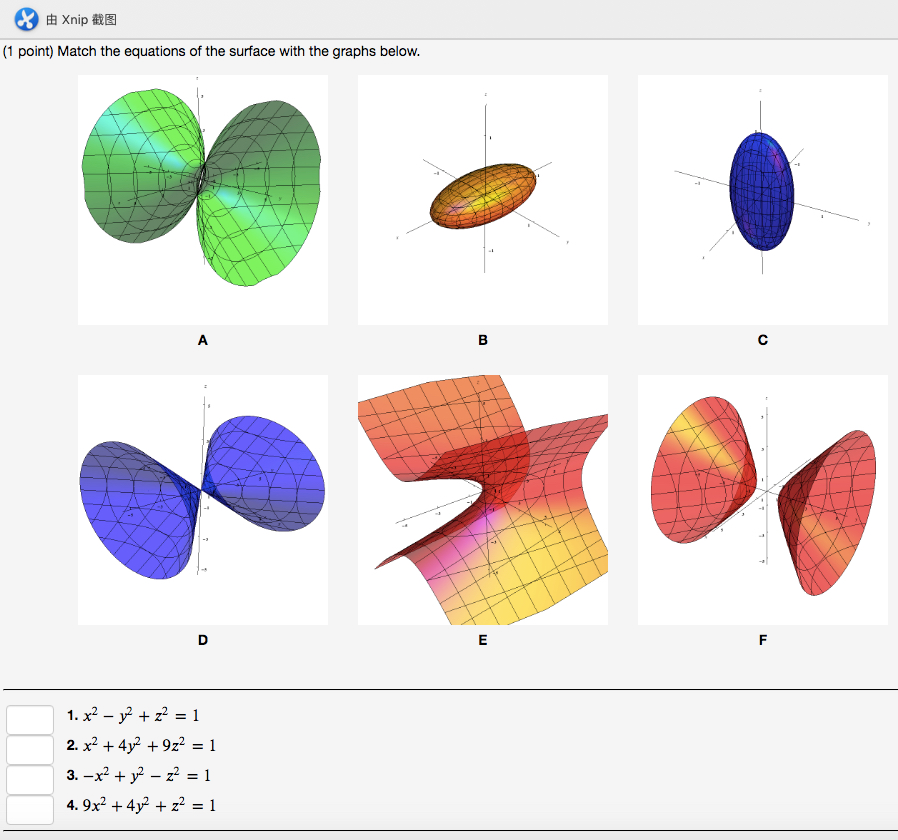
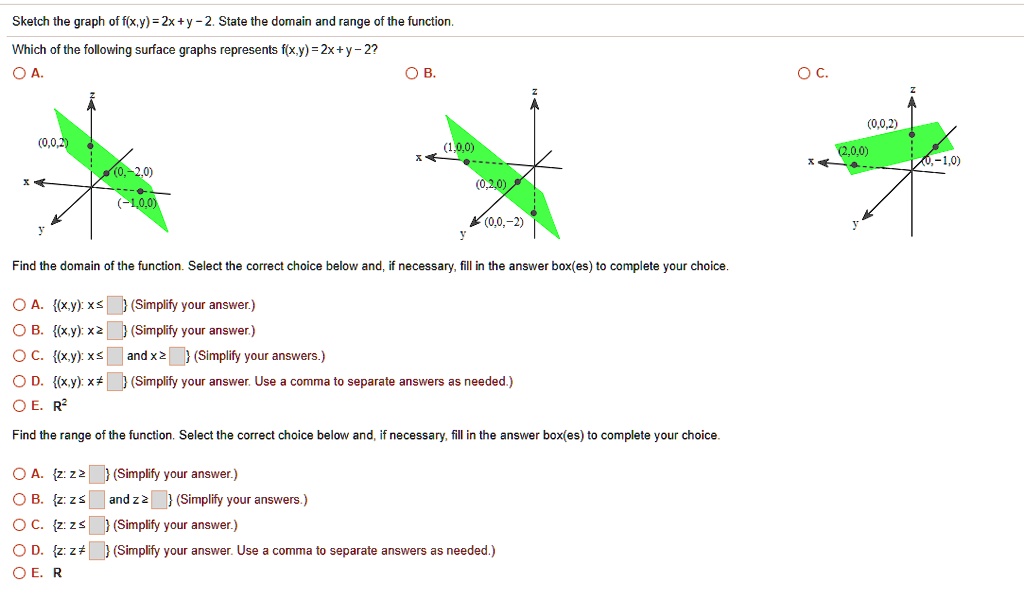
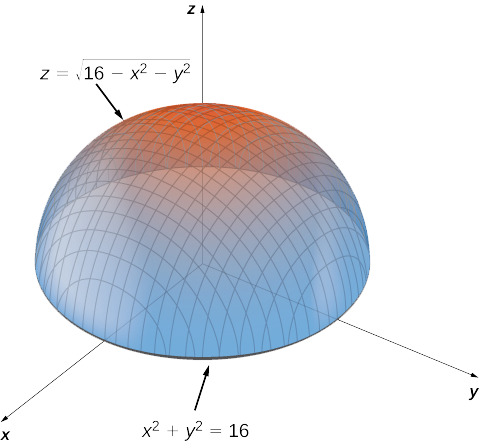
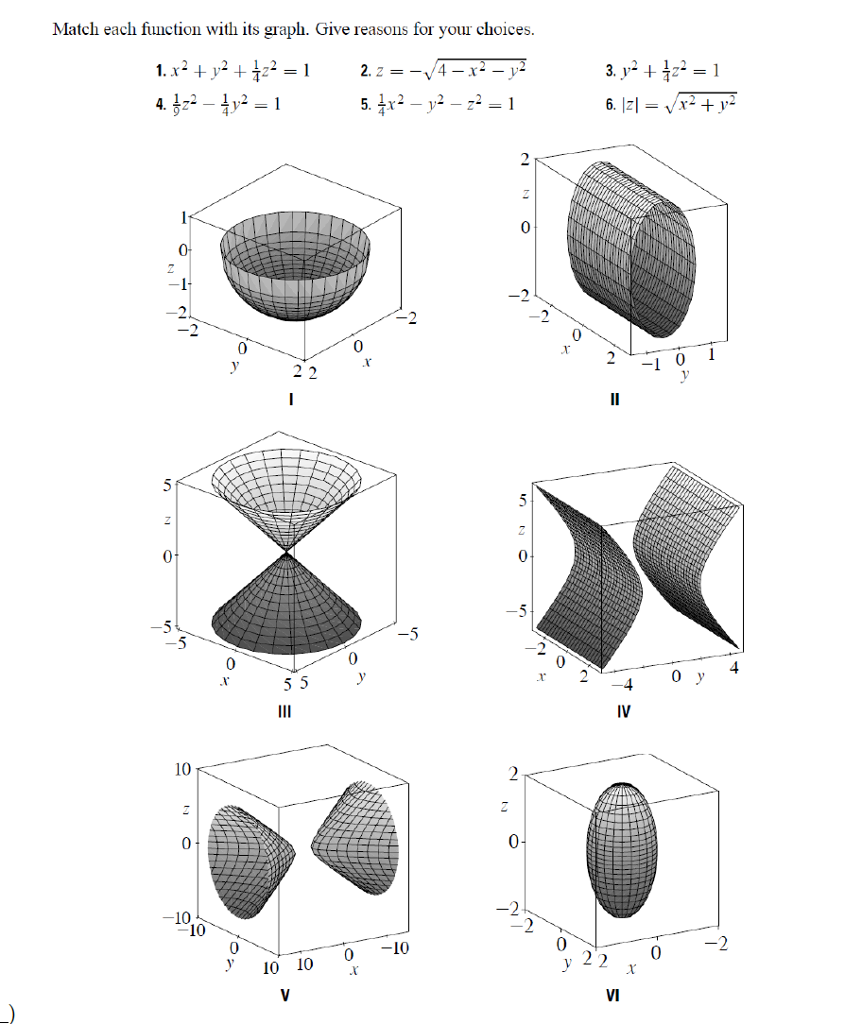
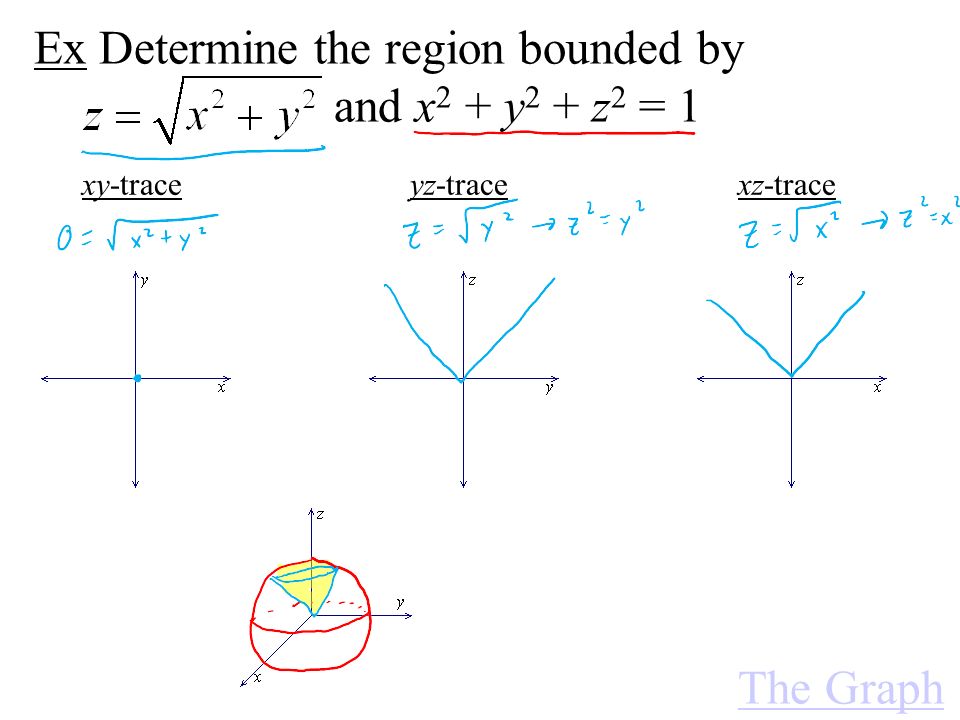
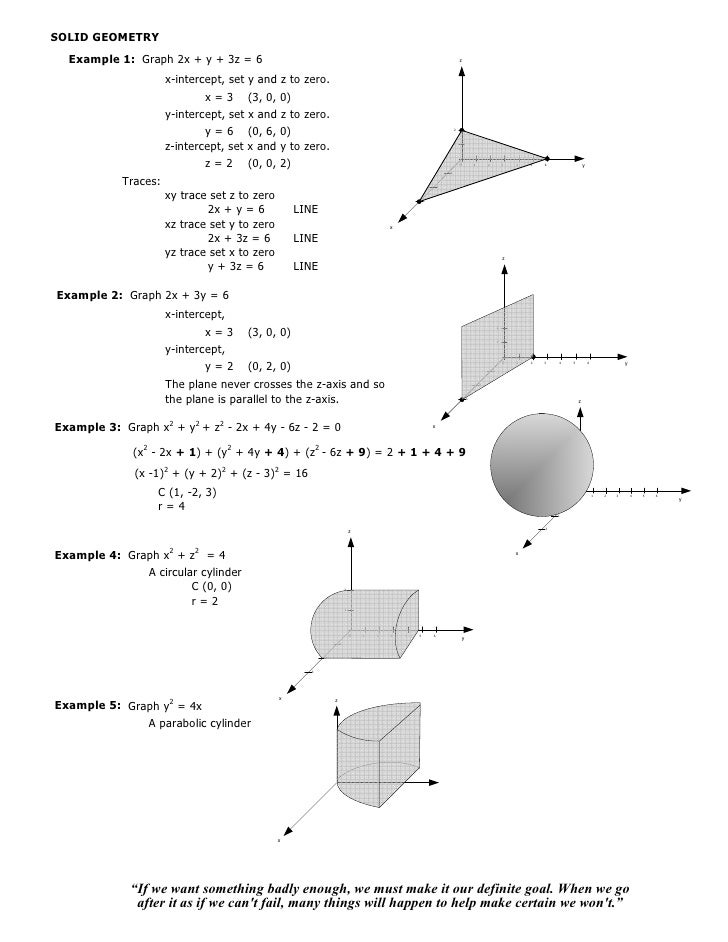
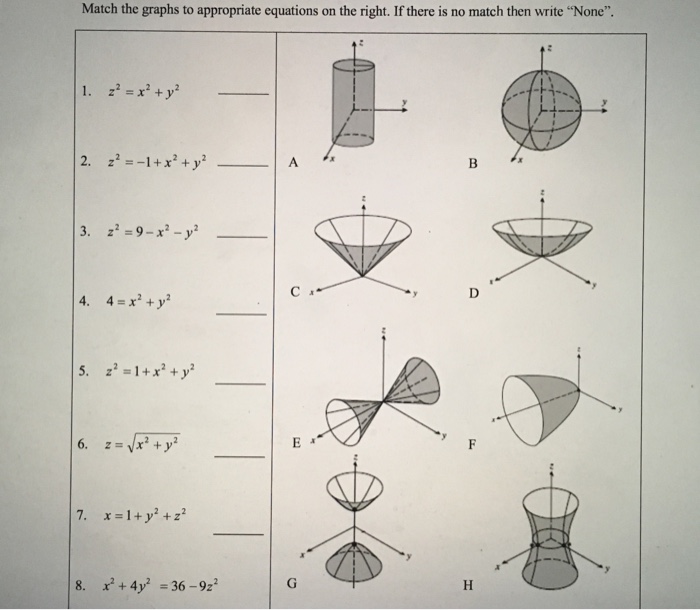
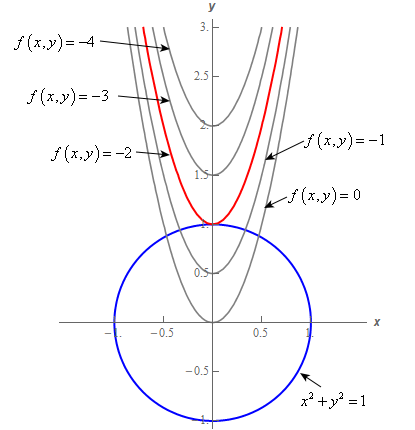
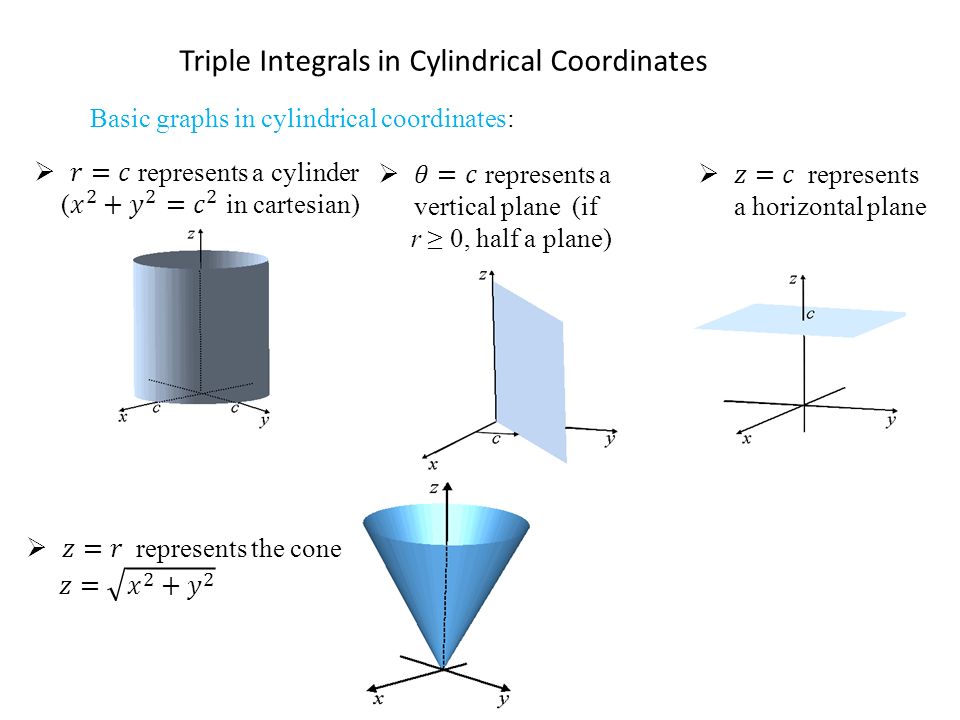
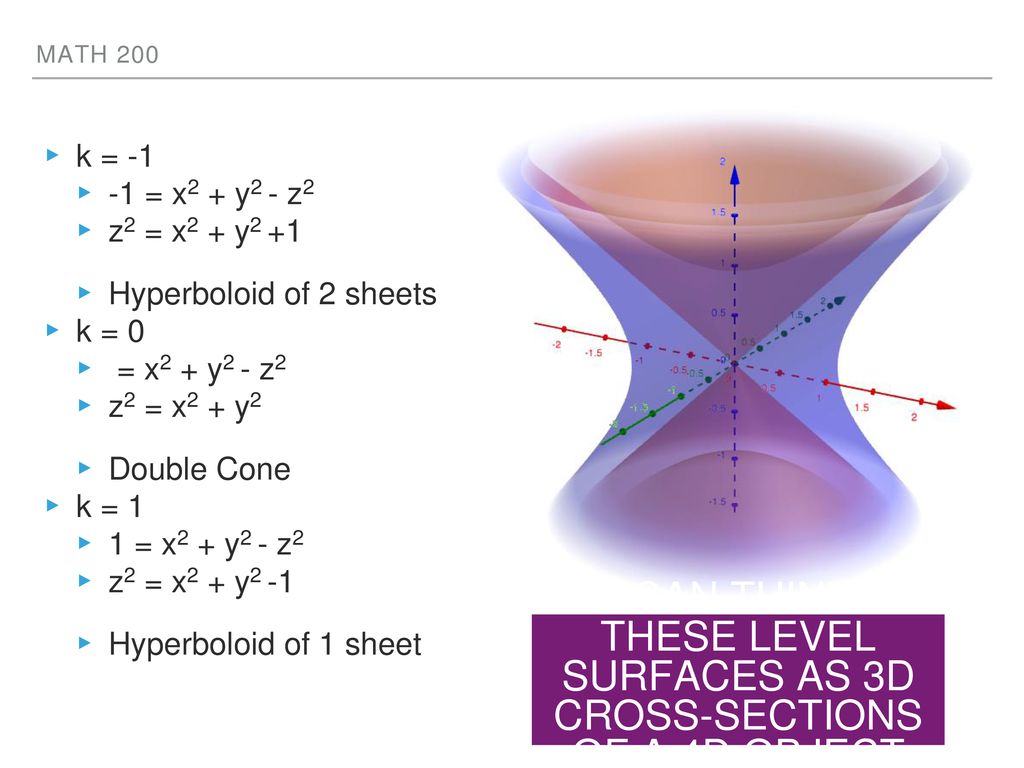
(e) Below is the graph of z = x2 y2 On the graph of the surface, sketch the traces that you found in parts (a) and (c) For problems 1213, nd an equation of the trace of the surface in the indicated plane Describe the graph of the trace 12 Surface 8x 2 y z2 = 9;Graphs (z= f(x;y)) The graph of f R2!R is f(x;y;z) 2R3 jz= f(x;y)g Example When we say \the surface z= x2 y2," we really mean \The graph of the function f(x;y) = x2 y2" That is, we mean the set f(x;y;z) 2R3 jz= x2 y2g Level Sets (F(x;y;z) = c) The level set of F R3!R at height cis f(x;y;z) 2R3 jF(x;y;z) = cg
Incoming Term: x^2+y^2+z^2=r^2 graph,




0 件のコメント:
コメントを投稿